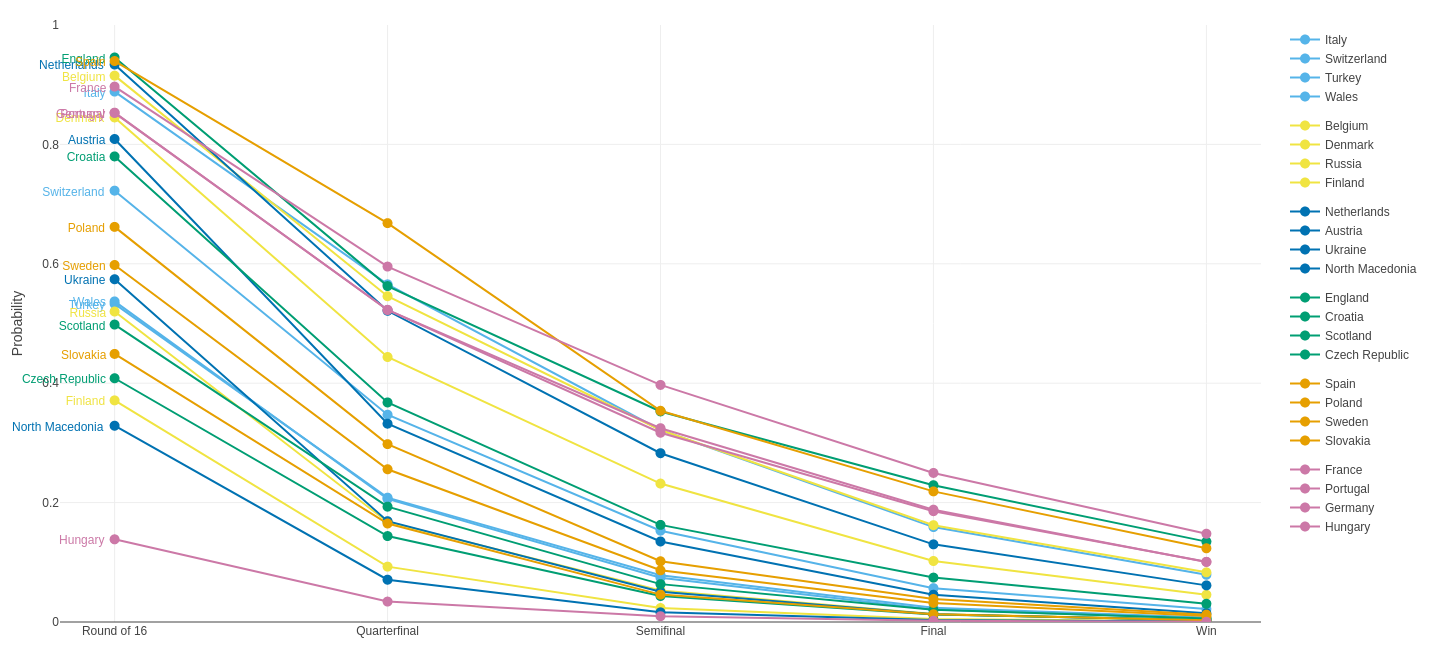Hybrid machine learning forecasts for the UEFA Euro 2020
Winning probabilities
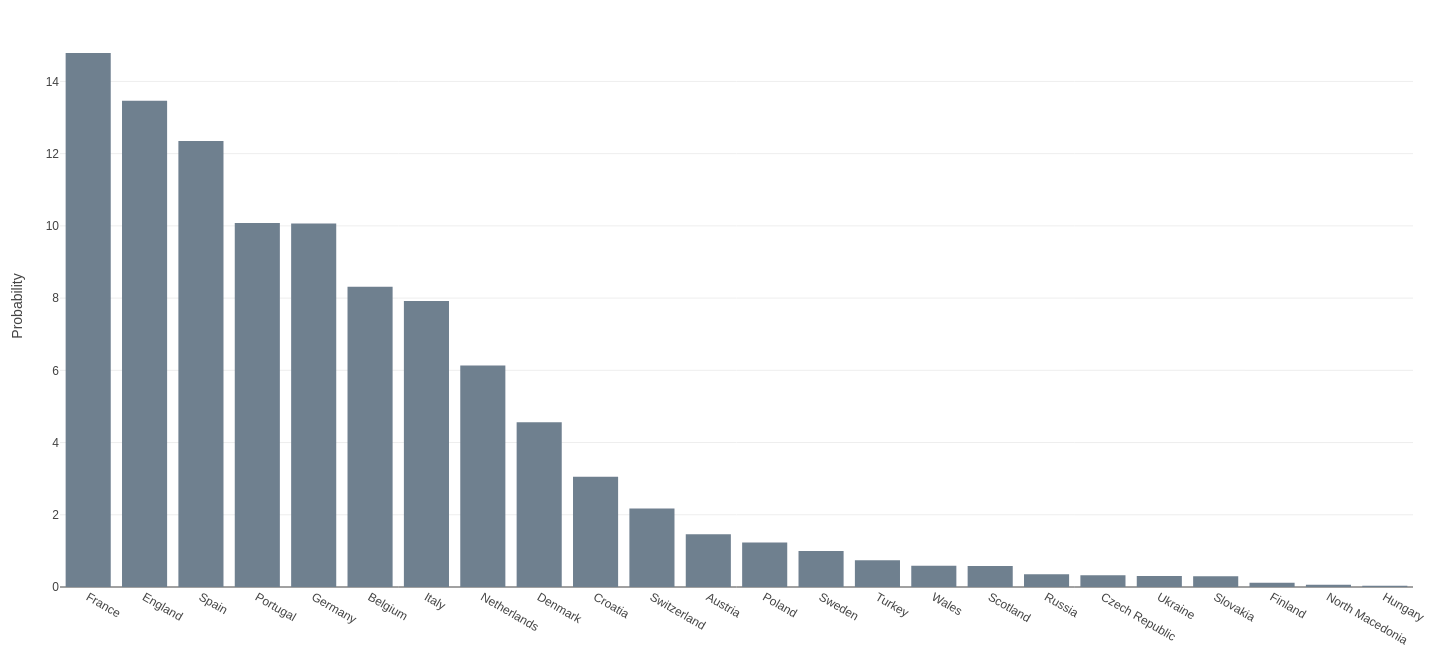
The forecast is based on a conditional inference random forest learner that combines four main sources of information: An ability estimate for every team based on historic matches; an ability estimate for every team based on odds from 19 bookmakers; average ratings of the players in each team based on their individual performances in their home clubs and national teams; further team covariates (e.g., market value, team structure) and country-specific socio-economic factors (population, GDP). The random forest model is learned using the UEFA Euro tournaments from 2004 to 2016 as training data and then applied to current information to obtain a forecast for the UEFA Euro 2020. The random forest forecasts actually provide the predicted number of goals for each team in all possible matches in the tournament so that a bivariate Poisson distribution can be used to compute the probabilities for a win, draw, or loss in such a match. Based on these match probabilities the entire tournament can be simulated 100,000 times yielding winning probabilities for each team. The results show that the current World Champion France is also the favorite for the European title with a winning probability of 14.8%, followed by England with 13.5%, and Spain with 12.3%. The winning probabilities for all teams are shown in the barchart below with more information linked in the interactive full-width version.
Interactive full-width graphic
The full study has been conducted by an international team of researchers: Andreas Groll, Lars Magnus Hvattum, Christophe Ley, Franziska Popp, Gunther Schauberger, Hans Van Eetvelde, Achim Zeileis. The corresponding working paper will be published on arXiv in the next couple of days. The core of the contribution is a hybrid approach that starts out from four state-of-the-art forecasting methods, based on disparate sets of information, and lets an adaptive machine learning model decide how to best combine these forecasts.
-
Historic match abilities:
An ability estimate is obtained for every team based on “retrospective” data, namely all historic national matches over the last 8 years. A bivariate Poisson model with team-specific fixed effects is fitted to the number of goals scored by both teams in each match. However, rather than equally weighting all matches to obtain average team abilities (or team strengths) over the entire history period, an exponential weighting scheme is employed. This assigns more weight to more recent results and thus yields an estimate of current team abilities. More details can be found in Ley, Van de Wiele, Van Eetvelde (2019). -
Bookmaker consensus abilities:
Another ability estimate for every team is obtained based on “prospective” data, namely the odds of 19 international bookmakers that reflect their expert expectations for the tournament. Using the bookmaker consensus model of Leitner, Zeileis, Hornik (2010), the bookmaker odds are first adjusted for the bookmakers’ profit margins (“overround”) and then averaged (on a logit scale) to obtain a consensus for the winning probability of each team. To adjust for the effects of the tournament draw (that might have led to easier or harder groups for some teams), an “inverse” simulation approach is used to infer which team abilities are most likely to lead up to these winning probabilities. -
Average player ratings:
To infer the contributions of individual players in a match, the plus-minus player ratings of Hvattum (2019) dissect all matches with a certain player (both on club and on national level) into segments, e.g., between substitutions. Subsequently, the goal difference achieved in these segments is linked to the presence of the individual players during that segment. This yields individual ratings for all players that can be aggregated to average player ratings for each team. -
Hybrid random forests:
Finally, machine learning is used to combine these three highly aggregated and informative variables above along with a broad range of further relevant covariates, yielding refined probabilistic forecasts for each match. Such a hybrid approach was first suggested by Groll, Ley, Schauberger, Van Eetvelde (2019). The task the random forest learner has to accomplish is to combine the three highly-informative team variables above with further team-specific information that may or may not be relevant to the team’s performance. The covariates considered comprise team-specific details (e.g., market value, FIFA rank, team structure) as well as country-specifc socio-economic factors (population and GDP per capita). By combining a large ensemble of rather weakly informative regression trees in a random forest, the relative importances of all the covariates can be inferred automatically. The resulting predicted number of goals for each team can then finally be used to simulate the entire tournament 100,000 times.
Match probabilities
Using the hybrid random forest an expected number of goals is obtained for both teams in each possible match. The covariate information used for this is the difference between the two teams in each of the variables listed above, i.e., the difference in historic match abilities (on a log scale), the difference in bookmaker consensus abilities (on a log scale), difference in average player ratings of the teams, etc. Assuming a bivariate Poisson distribution with the expected numbers of goals for both teams, we can compute the probability that a certain match ends in a win, a draw, or a loss. The same can be repeated in overtime, if necessary, and a coin flip is used to decide penalties, if needed.
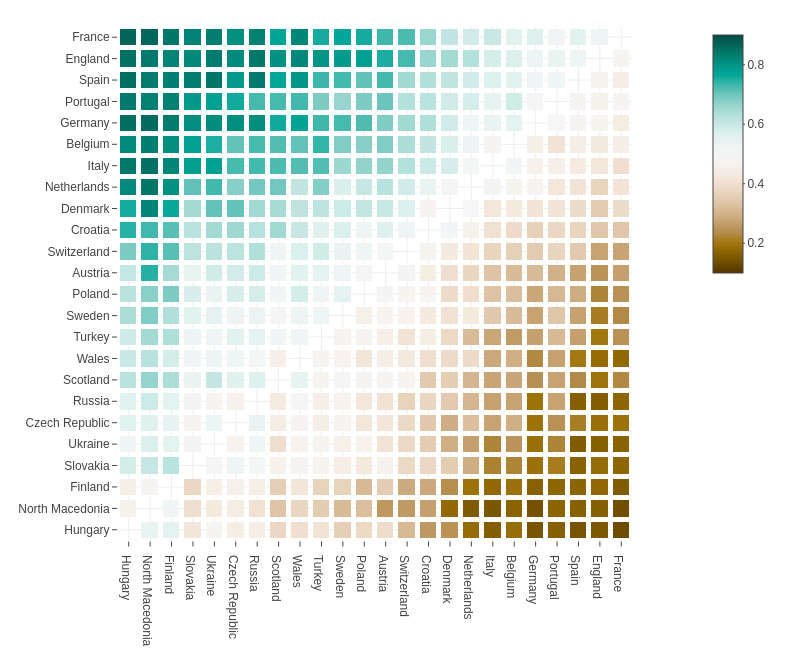
The following heatmap shows for each possible combination of teams the probability that one team beats the other team in a knockout match. The color scheme uses green vs. brown to signal probabilities above vs. below 50%, respectively. The tooltips for each match in the interactive version of the graphic also print the probabilities for the match to end in a win, draw, or loss after normal time.
Interactive full-width graphic
Performance throughout the tournament
As every single match can be simulated with the pairwise probabilities above, it is also straightfoward to simulate the entire tournament (here: 100,000 times) providing “survival” probabilities for each team across the different stages.
Interactive full-width graphic
Odds and ends
All our forecasts are probabilistic, clearly below 100%, and thus by no means certain. Especially the results in group F are hard to predict but may play a crucial role for the tournament. The reason is that this group comprises three very strong teams with current World Champion France, defending European Champion Portugal, and Germany which generally has an excellent record at international tournaments. Moreover, the runner-up in this group will play against the winner from group D with favorite England. Hence, it is likely that this will lead to a very tough knockout match in the round of 16, possibly even between the two top favorites France and England, but it is hard to predict the exact pair of teams that will face each other in this match.
Another interesting observation is that the winning probability for Belgium is only moderately high with 8.3%. This is notable as Belgium currently leads the FIFA/Coca-Cola World Ranking and is also judged to have a much higher winning probability by the bookmaker consensus model with 12.1%.
In any case, all of this means that even when we can quantify in terms of probabilities what is likely to happen during the UEFA Euro 2020, it is far from being predetermined. Hence, we can all look forward to finally watching this exciting tournament and hope it will bring a little bit of the joy that we have been missing over this difficult last year.