ivreg: Two-stage least-squares regression with diagnostics
Package overview
The ivreg package (by John Fox,
Christian Kleiber, and
Achim Zeileis) provides a comprehensive implementation of instrumental variables
regression using two-stage least-squares (2SLS) estimation. The standard
regression functionality (parameter estimation, inference, robust covariances,
predictions, etc.) is derived from and supersedes the ivreg() function in the
AER package. Additionally, various
regression diagnostics are supported, including hat values, deletion diagnostics such
as studentized residuals and Cook’s distances; graphical diagnostics such as
component-plus-residual plots and added-variable plots; and effect plots with partial
residuals.
An overview of the package along with vignettes and detailed documentation etc. is available on its web site at https://john-d-fox.github.io/ivreg/. This post is an abbreviated version of the “Getting started” vignette.
The ivreg package integrates seamlessly with other packages by providing suitable S3 methods, specifically for generic functions in the base-R stats package, and in the car, effects, lmtest, and sandwich packages, among others. Moreover, it cooperates well with other object-oriented packages for regression modeling such as broom and modelsummary.
Illustration: Returns to schooling
For demonstrating the ivreg package in practice, we investigate
the effect of schooling on earnings in a classical model for wage determination.
The data are from the United States, and are provided in the package as
SchoolingReturns. This data set was originally studied by David Card, and was subsequently
employed, as here, to illustrate 2SLS estimation in introductory econometrics textbooks.
The relevant variables for this illustration are:
data("SchoolingReturns", package = "ivreg")
summary(SchoolingReturns[, 1:8])
## wage education experience ethnicity smsa
## Min. : 100.0 Min. : 1.00 Min. : 0.000 other:2307 no : 864
## 1st Qu.: 394.2 1st Qu.:12.00 1st Qu.: 6.000 afam : 703 yes:2146
## Median : 537.5 Median :13.00 Median : 8.000
## Mean : 577.3 Mean :13.26 Mean : 8.856
## 3rd Qu.: 708.8 3rd Qu.:16.00 3rd Qu.:11.000
## Max. :2404.0 Max. :18.00 Max. :23.000
## south age nearcollege
## no :1795 Min. :24.00 no : 957
## yes:1215 1st Qu.:25.00 yes:2053
## Median :28.00
## Mean :28.12
## 3rd Qu.:31.00
## Max. :34.00
A standard wage equation uses a semi-logarithmic linear regression for wage, estimated by
ordinary least squares (OLS), with years of education as the primary explanatory variable,
adjusting for a quadratic term in labor-market experience, as well as for factors
coding ethnicity, residence in a city (smsa), and residence in the U.S. south:
m_ols <- lm(log(wage) ~ education + poly(experience, 2) + ethnicity + smsa + south,
data = SchoolingReturns)
summary(m_ols)
## Call:
## lm(formula = log(wage) ~ education + poly(experience, 2) + ethnicity +
## smsa + south, data = SchoolingReturns)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.59297 -0.22315 0.01893 0.24223 1.33190
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.259820 0.048871 107.626 < 2e-16 ***
## education 0.074009 0.003505 21.113 < 2e-16 ***
## poly(experience, 2)1 8.931699 0.494804 18.051 < 2e-16 ***
## poly(experience, 2)2 -2.642043 0.374739 -7.050 2.21e-12 ***
## ethnicityafam -0.189632 0.017627 -10.758 < 2e-16 ***
## smsayes 0.161423 0.015573 10.365 < 2e-16 ***
## southyes -0.124862 0.015118 -8.259 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3742 on 3003 degrees of freedom
## Multiple R-squared: 0.2905, Adjusted R-squared: 0.2891
## F-statistic: 204.9 on 6 and 3003 DF, p-value: < 2.2e-16
Thus, OLS estimation yields an estimate of 7.4%
per year for returns to schooling. This estimate is problematic, however, because it can be argued
that education is endogenous (and hence also experience, which is taken to be age minus
education minus 6). We therefore use geographical proximity to a college when growing
up as an exogenous instrument for education. Additionally, age is the natural
exogenous instrument for experience, while the remaining explanatory variables can be considered
exogenous and are thus used as instruments for themselves.
Although it’s a useful strategy to select an effective instrument or instruments for each endogenous
explanatory variable, in 2SLS regression all of the instrumental variables are used to estimate all
of the regression coefficients in the model.
To fit this model with ivreg() we can simply extend the formula from lm() above, adding a second
part after the | separator to specify the instrumental variables:
library("ivreg")
m_iv <- ivreg(log(wage) ~ education + poly(experience, 2) + ethnicity + smsa + south |
nearcollege + poly(age, 2) + ethnicity + smsa + south,
data = SchoolingReturns)
Equivalently, the same model can also be specified slightly more concisely using three parts on the right-hand side indicating the exogenous variables, the endogenous variables, and the additional instrumental variables only (in addition to the exogenous variables).
m_iv <- ivreg(log(wage) ~ ethnicity + smsa + south | education + poly(experience, 2) |
nearcollege + poly(age, 2), data = SchoolingReturns)
Both models yield the following results:
summary(m_iv)
## Call:
## ivreg(formula = log(wage) ~ education + poly(experience, 2) +
## ethnicity + smsa + south | nearcollege + poly(age, 2) + ethnicity +
## smsa + south, data = SchoolingReturns)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.82400 -0.25248 0.02286 0.26349 1.31561
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.48522 0.67538 6.641 3.68e-11 ***
## education 0.13295 0.05138 2.588 0.009712 **
## poly(experience, 2)1 9.14172 0.56350 16.223 < 2e-16 ***
## poly(experience, 2)2 -0.93810 1.58024 -0.594 0.552797
## ethnicityafam -0.10314 0.07737 -1.333 0.182624
## smsayes 0.10798 0.04974 2.171 0.030010 *
## southyes -0.09818 0.02876 -3.413 0.000651 ***
##
## Diagnostic tests:
## df1 df2 statistic p-value
## Weak instruments (education) 3 3003 8.008 2.58e-05 ***
## Weak instruments (poly(experience, 2)1) 3 3003 1612.707 < 2e-16 ***
## Weak instruments (poly(experience, 2)2) 3 3003 174.166 < 2e-16 ***
## Wu-Hausman 2 3001 0.841 0.432
## Sargan 0 NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4032 on 3003 degrees of freedom
## Multiple R-Squared: 0.1764, Adjusted R-squared: 0.1747
## Wald test: 148.1 on 6 and 3003 DF, p-value: < 2.2e-16
Thus, using two-stage least squares to estimate the regression yields a much larger
coefficient for the returns to schooling, namely 13.3% per year.
Notice as well that the standard errors of the coefficients are larger for 2SLS estimation
than for OLS, and that, partly as a consequence, evidence for the effects of ethnicity
and the quadratic component of experience is now weak. These differences are brought
out more clearly when showing coefficients and standard errors side by side, e.g., using the
compareCoefs() function from the car package or the msummary() function from the
modelsummary package:
library("modelsummary")
m_list <- list(OLS = m_ols, IV = m_iv)
msummary(m_list)
| OLS | IV | |
|---|---|---|
| (Intercept) | 5.260 (0.049) |
4.485 (0.675) |
| education | 0.074 (0.004) |
0.133 (0.051) |
| poly(experience, 2)1 | 8.932 (0.495) |
9.142 (0.564) |
| poly(experience, 2)2 | -2.642 (0.375) |
-0.938 (1.580) |
| ethnicityafam | -0.190 (0.018) |
-0.103 (0.077) |
| smsayes | 0.161 (0.016) |
0.108 (0.050) |
| southyes | -0.125 (0.015) |
-0.098 (0.029) |
| Num.Obs. | 3010 | 3010 |
| R2 | 0.291 | 0.176 |
| R2 Adj. | 0.289 | 0.175 |
| AIC | 2633.4 | |
| BIC | 2681.5 | |
| Log.Lik. | -1308.702 | |
| F | 204.932 |
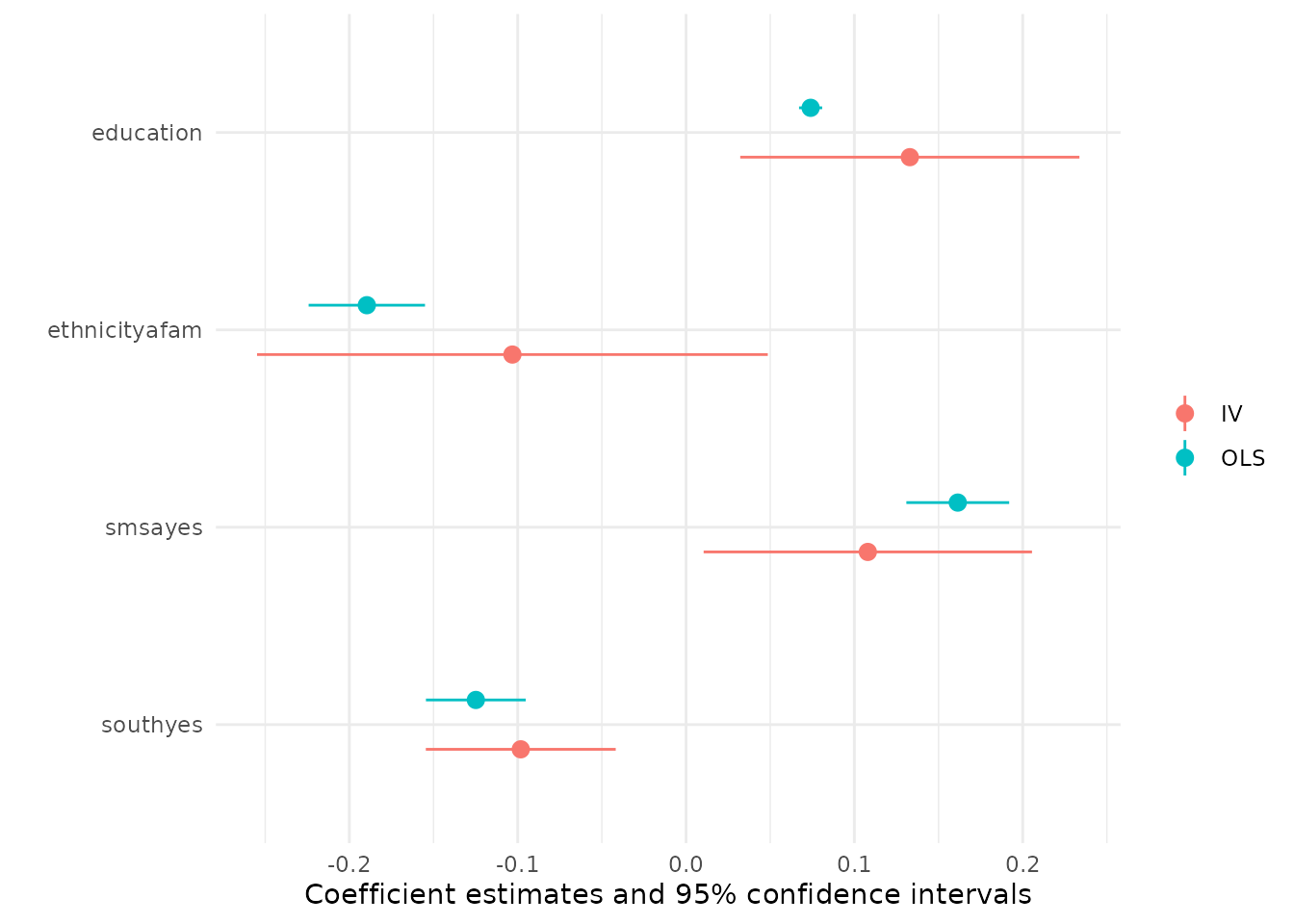
The change in coefficients and associated standard errors can also be brought out graphically
using the modelplot() function from modelsummary which shows the coefficient estimates
along with their 95% confidence intervals. Below we omit the intercept and experience terms
as these are on a different scale than the other coefficients.
modelplot(m_list, coef_omit = "Intercept|experience")