Network trees: networktree 1.0.0, web page, and Psychometrika paper
Psychometrika paper
- Citation: Jones PJ, Mair P, Simon T, Zeileis A (2020). “Network Trees: A Method for Recursively Partitioning Covariance Structures.” Psychometrika, 85(4), 926-945. doi:10.1007/s11336-020-09731-4.
- Preprint version: https://www.zeileis.org/papers/Jones+Mair+Simon-2020.pdf
- OSF replication materials: https://osf.io/ykq2a/
Abstract
In many areas of psychology, correlation-based network approaches (i.e., psychometric networks) have become a popular tool. In this paper, we propose an approach that recursively splits the sample based on covariates in order to detect significant differences in the structure of the covariance or correlation matrix. Psychometric networks or other correlation-based models (e.g., factor models) can be subsequently estimated from the resultant splits. We adapt model-based recursive partitioning and conditional inference tree approaches for finding covariate splits in a recursive manner. The empirical power of these approaches is studied in several simulation conditions. Examples are given using real-life data from personality and clinical research.
Software & web page
All methods discussed are implemented in the R package networktree that is developed on GitHub and stable versions are released on CRAN (Comprehensive R Archive Network). Version 1.0.0 accompanies the publications in Psychometrika and version 1.0.1 adds a few small enhancements and bug fixes, specifically for the plotting infrastructure. Furthermore, a nice web page with introductory examples, documentation, release notes, etc. has been produced with the wonderful pkgdown.
- CRAN release: https://CRAN.R-project.org/package=networktree
- Web page: https://paytonjjones.github.io/networktree/
Illustration
The idea of psychometric networks is to provide information about the statistical relationships between observed variables. Network trees aim to reveal heterogeneities in these relationships based on observed covariates. This strategy is implemented in the R package networktree building on the general tree algorithms in the partykit package.
For illustration, we consider a depression network - where the nodes represent different symptoms - and detect heterogeneities with respect to age and race. The data used below is provided by https://openpsychometrics.org/ and was obtained using the Depression Anxiety and Stress Scale (DASS), a self-report instrument for measuring depression, anxiety, and tension or stress. It is available in the networktree package as dass. To make resulting graphics and summaries easier to interpret we use the following variable names for the depression symptoms that are measured with certain questions from the DASS:
anhedonia(Question 3: I couldn’t seem to experience any positive feeling at all.)initiative(Question 42: I found it difficult to work up the initiative to do things.)lookforward(Question 10: I felt that I had nothing to look forward to.)sad(Question 13: I felt sad and depressed.)unenthused(Question 31: I was unable to become enthusiastic about anything.)worthless(Question 17: I felt I wasn’t worth much as a person.)meaningless(Question 38: I felt that life was meaningless.)
First, we load the data and relabel the variables for the depression symptoms:
library("networktree")
data("dass", package = "networktree")
names(dass)[c(3, 42, 10, 13, 31, 17, 38)] <- c("anhedonia", "initiative", "lookforward",
"sad", "unenthused", "worthless", "meaningless")
Subsequently, we fit a networktree() where the relationship between the symptoms (anhedonia + initiative + lookforward + sad + unenthused + worthless + meaningless) is “explained by” (~) the covariates (age + race). (As an alternative to this formula-based interface it is also possible to specify groups of dependent and split variables, respectively, through separate data frames.) The threshold for detecting significant differences in correlations is set to 1% (plus Bonferroni adjustment for testing two covariates at each step).
tr <- networktree(anhedonia + initiative + lookforward + sad + unenthused +
worthless + meaningless ~ age + race, data = dass, alpha = 0.01)
The resulting network tree can be easily visualized with plot(tr) which would display the raw correlations. As these are generally high between all depression symptoms we use a display with partial correlations (transform = "pcor") instead. This brings out differences between the detected subgroups somewhat more clearly. (Note that version 1.0.1 of networktree is needed for this to work correctly.)
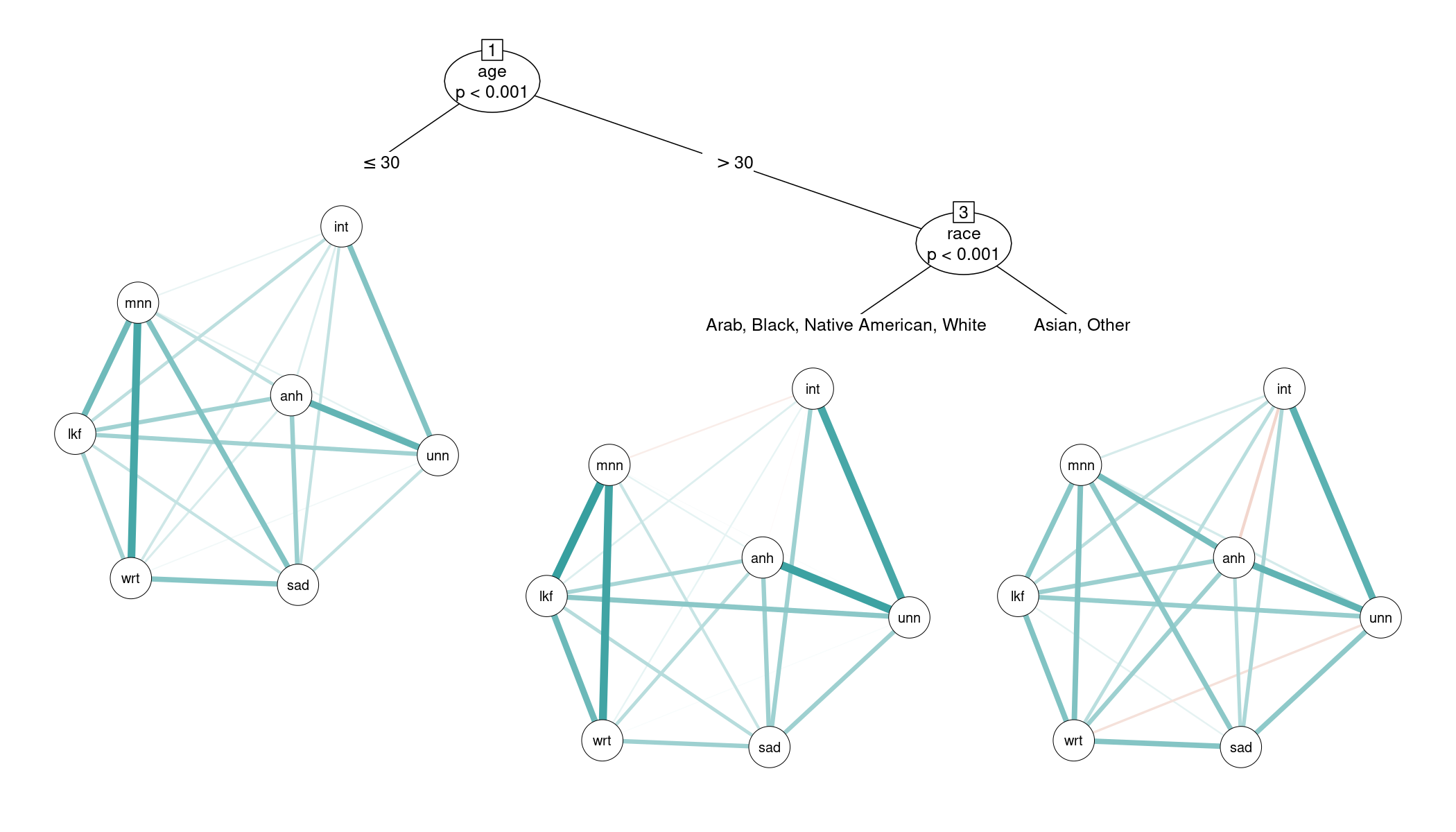
plot(tr, transform = "pcor")
This shows that the network tree detects three subgroups. First, the correlations of the depression symptoms change across age - with the largest difference between “younger” and “older” persons in the sample at a split point of 30 years. Second, the correlations differ with respect to race for the older persons in the sample - with the largest difference between Arab/Black/Native American/White and Asian/Other. The differences in the symptom correlations affect various pairs of symptoms as brought out in the network display produced by the qgraph package in the terminal nodes. For example, the “centrality” of anhedonia changes across the three detected subgroups: For the older Asian/Other persons it is partially correlated with most other symptoms while this is less pronounced for the other two subgroups.
The networks visualized in the tree can also be extracted easily using the getnetwork() function. For example, the partial correlation matrix corresponding to the older Asian/Other group (node 5) can be obtained by:
getnetwork(tr, id = 5, transform = "pcor")
To explore the returned object tr in some more detail, the print() method gives a printed version of the tree structure but does not display the associated parameters.
tr
## Network tree object
##
## Model formula:
## anhedonia + initiative + lookforward + sad + unenthused + worthless +
## meaningless ~ age + race
##
## Fitted party:
## [1] root
## | [2] age <= 30
## | [3] age > 30
## | | [4] race in Arab, Black, Native American, White
## | | [5] race in Asian, Other
##
## Number of inner nodes: 2
## Number of terminal nodes: 3
## Number of parameters per node: 21
## Objective function: 42301.84
The estimated correlation parameters in the subgroups can be extracted with coef(tr), here returning a 3 x 21 matrix for the 21 pairs of symptom correlations and the 3 subgroups. To show two symptom pairs with larger correlation differences we extract the correlations of anhedonia with worthless and meaningless, respectively. Note that these are the raw correlations and not the partial correlations displayed in the tree above.
coef(tr)[, 5:6]
## rho_anhedonia_worthless rho_anhedonia_meaningless
## 2 0.5595725 0.5994682
## 4 0.6741686 0.6339481
## 5 0.6639088 0.7178744
Finally, we extract the p-values of the underlying parameter instability tests to gain some insights how the tree was constructed. In each step the stability we assess whether the correlation parameters are stable across each of the two covariates age and race or whether there are significant changes. The corresponding test statistics and Bonferroni-adjusted p-values can be extracted with the sctest() function (for “structural change test”). For example, in Node 1 there are significant instabilities with respect to both variables but age has the lower p-value and is hence selected for partitioning the data:
library("strucchange")
sctest(tr, node = 1)
## age race
## statistic 7.151935e+01 1.781216e+02
## p.value 1.787983e-05 3.108049e-03
In Node 3 only race is significant and hence used for splitting:
sctest(tr, node = 3)
## age race
## statistic 42.9352852 1.728898e+02
## p.value 0.1447818 6.766197e-05
And in Node 5 neither variable is significant and hence the splitting stops:
sctest(tr, node = 5)
## age race
## statistic 35.1919522 22.09555
## p.value 0.5514142 0.63279
For more details regarding the method and the software see the Psychometrika paper and the software web page, respectively.