Circular regression trees and forests
Citation
Lang MN, Schlosser L, Hothorn T, Mayr GJ, Stauffer R, Zeileis A (2020). “Circular Regression Trees and Forests with an Application to Probabilistic Wind Direction Forecasting”, arXiv:2001.00412, arXiv.org E-Print Archive. doi:10.48550/arXiv.2001.00412
Abstract
While circular data occur in a wide range of scientific fields, the methodology for distributional modeling and probabilistic forecasting of circular response variables is rather limited. Most of the existing methods are built on the framework of generalized linear and additive models, which are often challenging to optimize and interpret. Therefore, building on previous ideas for trees modeling circular means, we suggest a distributional approach for regression trees and random forests yielding probabilistic forecasts based on the von Mises distribution. The resulting tree-based models simplify the estimation process by using the available covariates for partitioning the data into sufficiently homogeneous subgroups so that a simple von Mises distribution without further covariates can be fitted to the circular response in each subgroup. These circular regression trees are straightforward to interpret, can capture nonlinear effects and interactions, and automatically select the relevant covariates that are associated with either location and/or scale changes in the von Mises distribution. Combining an ensemble of circular regression trees to a circular regression forest can regularize and smooth the covariate effects. The new methods are evaluated in a case study on probabilistic wind direction forecasting at two Austrian airports, considering other common approaches as a benchmark.
Software
R package circtree from the R-Forge project partykit: https://R-Forge.R-project.org/R/?group_id=261
Basic examples using artificial data:
install.packages("partykit")
install.packages("disttree", repos = "http://R-Forge.R-project.org")
install.packages("circtree", repos = "http://R-Forge.R-project.org")
library("circtree")
example("circtree", ask = FALSE)
vignette("circtree", package = "circtree")
Distributional approach
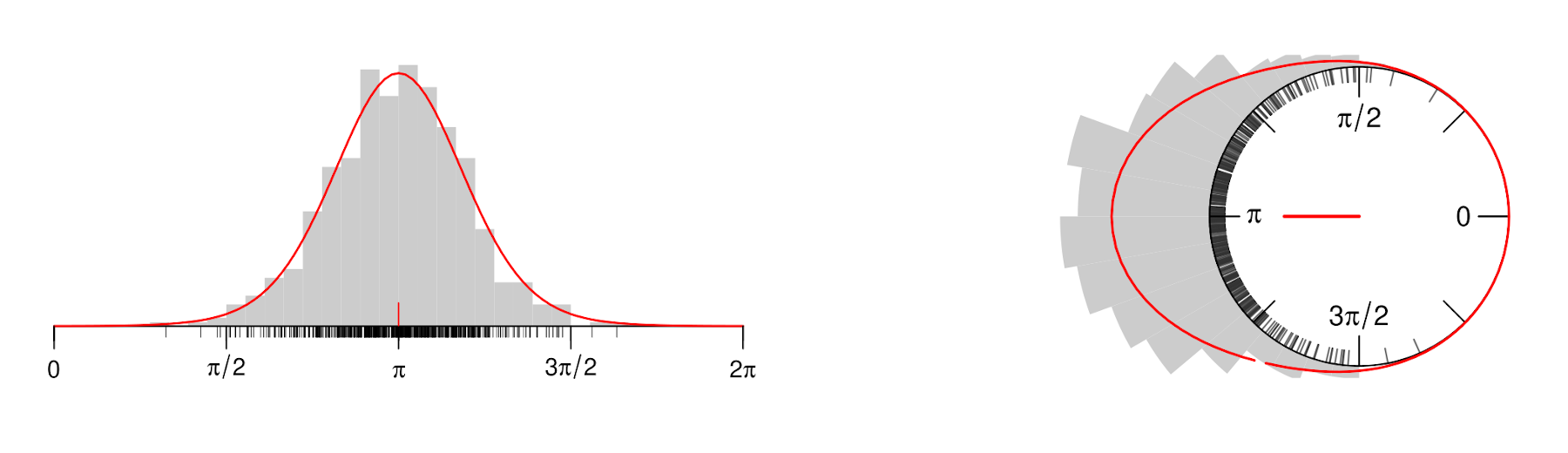
The basis for the proposed distributional modeling of the circular responses is the von Mises distribution, also known as the “circular normal distribution”. It is based on a location parameter μ in [0, 2 π) and a concentration parameter κ > 0.
The figure below illustrates a model, fitted by maximum likelihood, for circular data in the interval [0, 2 π). It can either be drawn on a linearized scale (left) or circular scale (right). In both cases the empirical histogram (gray bars) and fitted von Mises density (red line) are depicted along with the estimated location parameter (red hand).
The regression trees and forests extend this approach by employing an adaptive local likelihood approach: For each observation, the parameters μ and κ are estimated only locally in a neighborhood, defined either by the nodes of a single tree or weighted by the nodes of a forest.
Illustration
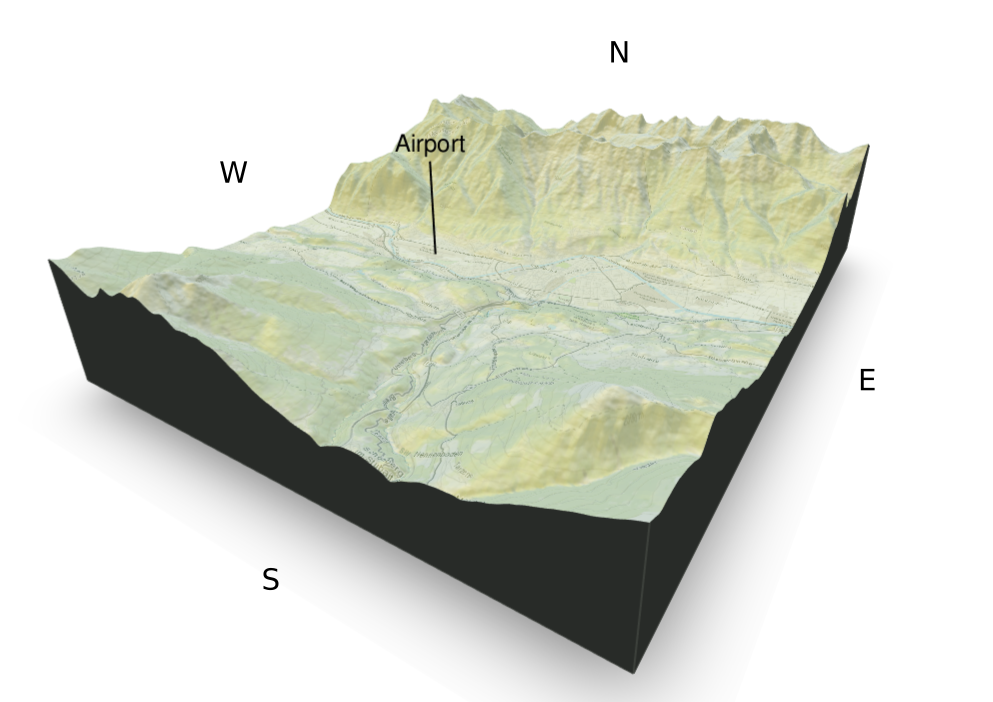
To provide a first impression of the methodology in practice (motivated by air traffic management), a circular regression tree is employed for probabilistic wind direction forecasting. More specifically, we obtain 1-hourly nowcasts of wind direction at Innsbruck Airport. As the airport is located at the bottom of a narrow valley within the European Alps, it is natural to employ tree-based regression models as there can be abrupt changes in the wind direction rather than smooth changes.
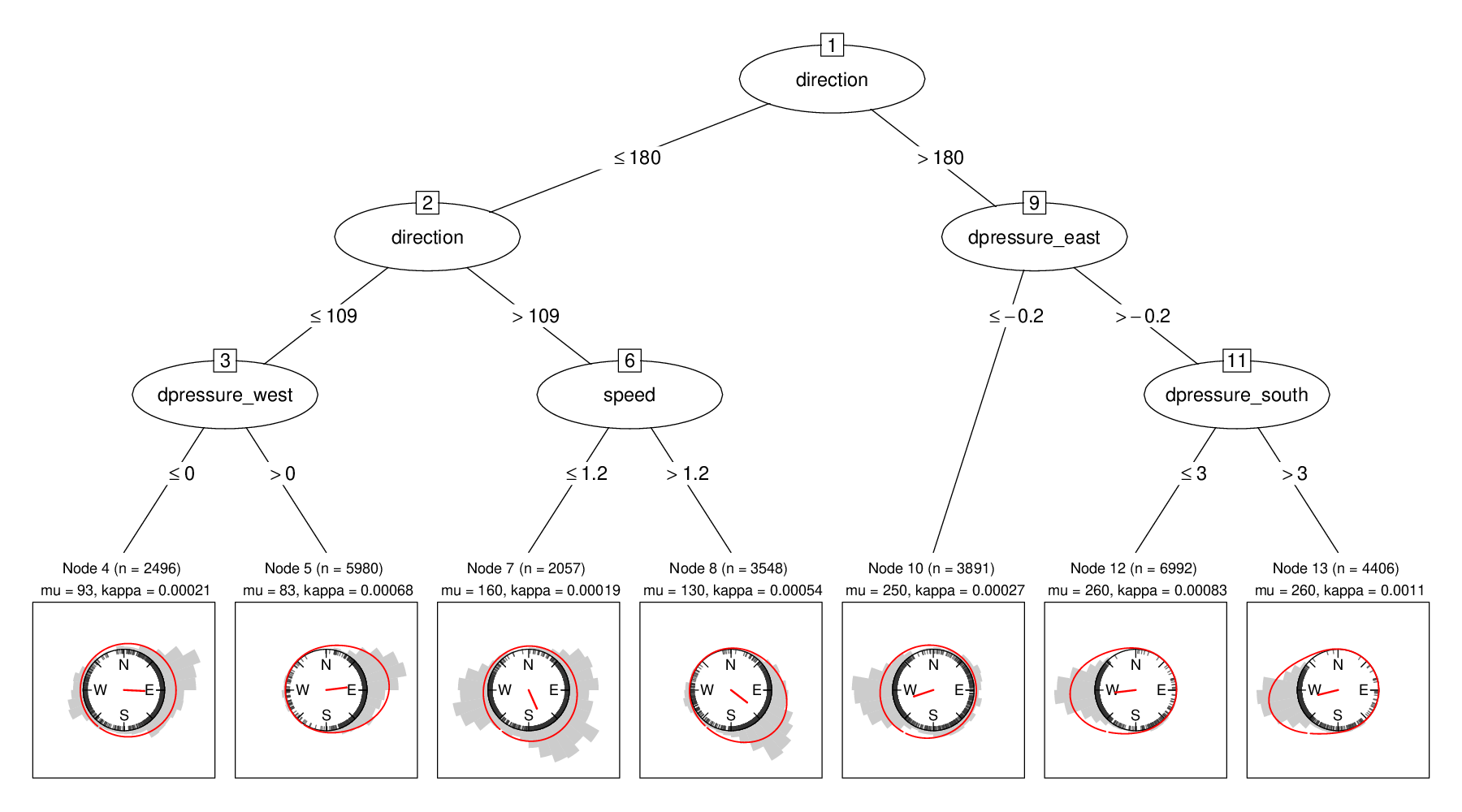
Due to the short lead time only observation data is employed for predictions (41,979 data points) but no numerical weather predictions. The data is obtained from 4 stations at Innsbruck Airport as well as 6 nearby weather stations. The base variables are: Wind direction, wind (gust) speed, temperature, (reduced) air pressure, relative humidity. Based on these 260 covariates are computed via means/minima/maxima, temporal changes, and spatial differences towards the airport. The resulting regression tree is shown below along with the empirical (gray) and fitted von Mises (red) wind direction distribution in each terminal node.
Based on the fitted location parameters μ, the subgroups can be distinguished into the following wind regimes:
- Up-valley winds blowing from the valley mouth towards the upper valley (from east to west, nodes 4 and 5).
- Downslope winds blowing across the Alpine crest along the intersecting valley towards Innsbruck (from south-east to north-west, node 8).
- Down-valley winds blowing in the direction of the valley mouth (from west to east, nodes 10, 12 and 13).
- Node 7 captures observations with rather low wind speeds that cannot be clearly distinguished into specific wind regimes and are consequently associated with a very low estimated concentration parameter κ, i.e., a high estimated variance.
In terms of covariates, the lagged wind “direction” (also known as “persistence”) is mostly responsible for distinguishing the broad range of wind regimes listed above while the pressure gradients and wind speed separate the data into subgroups with high vs. low precision.
A more extensive case study of circular regression trees and also circular random forests applied to probabilistic wind direction forecasting at Innsbruck Airport and Vienna International Airport is presented in Section 4 of the paper, along with a benchmark against commonly-used alternative approaches.