Personalized treatment effects with model4you
Citation
Heidi Seibold, Achim Zeileis, Torsten Hothorn (2019). “model4you: An R Package for Personalised Treatment Effect Estimation.” Journal of Open Research Software, 7(17), 1-6. doi:10.5334/jors.219
Abstract
Typical models estimating treatment effects assume that the treatment effect is the same for all individuals. Model-based recursive partitioning allows to relax this assumption and to estimate stratified treatment effects (model-based trees) or even personalised treatment effects (model-based forests). With model-based trees one can compute treatment effects for different strata of individuals. The strata are found in a data-driven fashion and depend on characteristics of the individuals. Model-based random forests allow for a similarity estimation between individuals in terms of model parameters (e.g. intercept and treatment effect). The similarity measure can then be used to estimate personalised models. The R package model4you implements these stratified and personalised models in the setting with two randomly assigned treatments with a focus on ease of use and interpretability so that clinicians and other users can take the model they usually use for the estimation of the average treatment effect and with a few lines of code get a visualisation that is easy to understand and interpret.
Software
https://CRAN.R-project.org/package=model4you
Illustration
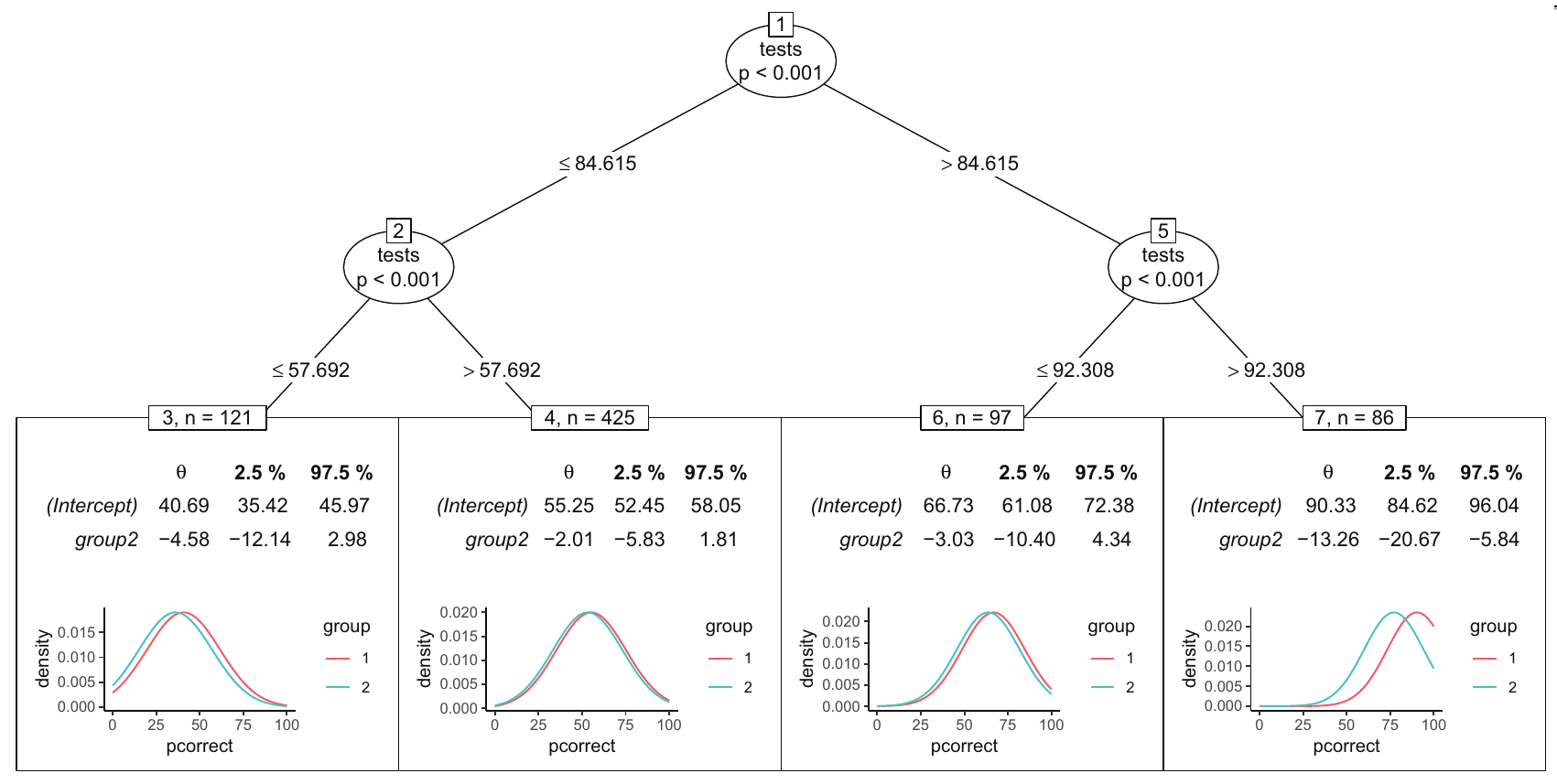
The correlation between exam group and exam performance in an introductory mathematics exam (for business and economics students) is investigated using tree-based stratified and personalized treatment effects. Group 1 took the exam in the morning and group 2 started the exam with slightly different exercises after the first group finished. Potential sources of heterogeneity in the group effect include gender, field of study, whether the exam was taken (and failed) previously, and prior performance in online “tests” earlier in the semester. Performance in both the written exam and the online tests is captured by percentage of correctly solved exercises.
Overall, it seems that the split into two different exam groups was fair: The second group had only a slightly lower performance by around 2 or 3 percentage points, suggesting that the exam in the second group was only very slightly more difficult. However, when investigating the heterogeneity of this group effect with a model-based tree it turns out that this distinguishes the students by their performance in the online tests. The largest difference between the two exam groups is in the students who did very well in the online tests (more than 92.3 percent correct), where the second-group students performed worse by 13.3 percentage points. So the split into the two exam groups seems to have been not fully fair for those very good students.
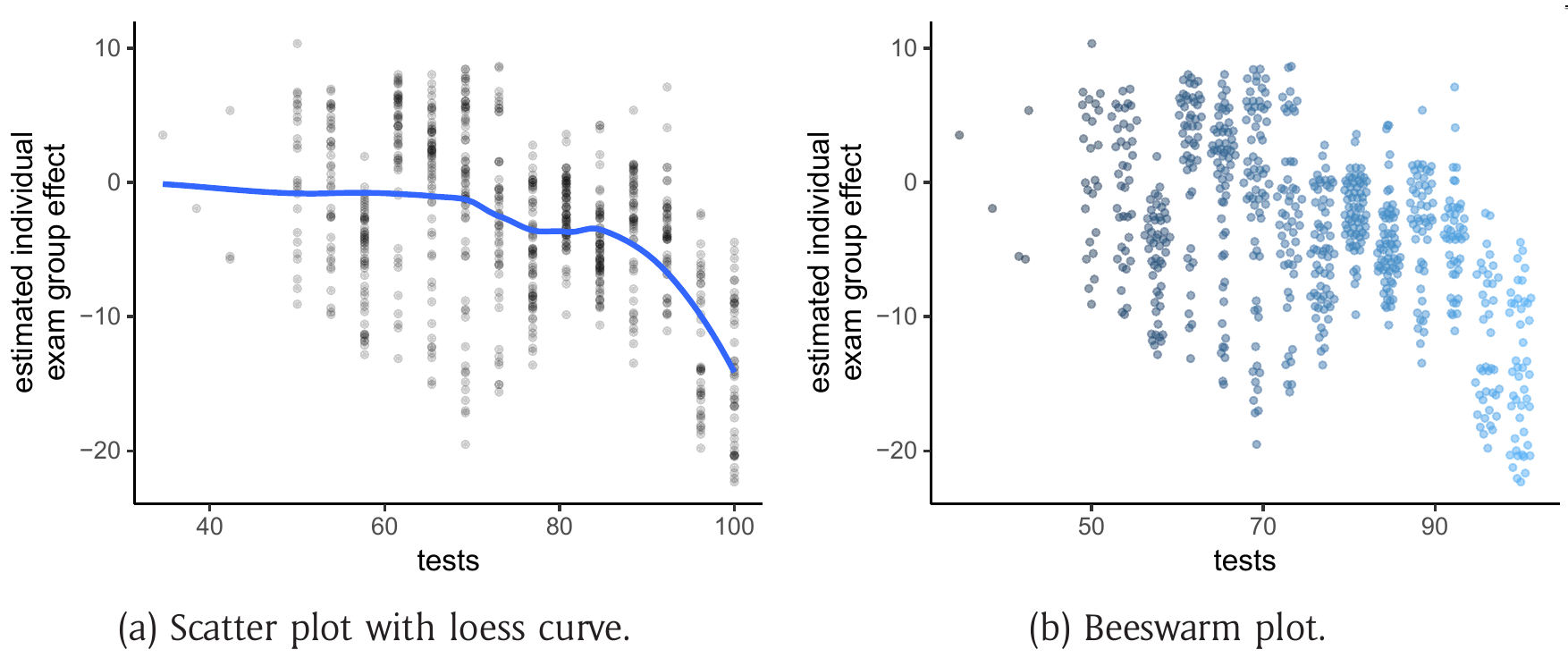
To refine the assessment further, a model-based forest can be estimated. This reveals that the dependence of the group effect on the performance in the online tests is even more pronounced. This is shown in the dependence plots and beeswarm plots below with the group treatment effect on the y-axis and the performance in the online tests on the x-axis.
To fit the simple linear base model in R, lm() can be used. The subsequent tree based on this model can be obtained with pmtree() from model4you and the forest with pmforest(). Example code is shown below, the full replication code for the entire analysis and graphics is included in the manuscript.
bmod_math <- lm(pcorrect ~ group, data = MathExam)
tr_math <- pmtree(bmod_math, control = ctree_control(maxdepth = 2))
forest_math <- pmforest(bmod_math)